|
||
| Release 4.0 | ||
 |
Formula Editor for LSystems
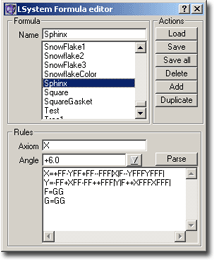
The goal of this chapter is to explain the formula editor window for Lindenmayer systems. So if you have questions concerning the theoretical background, please read chapter LSystem Theory.
The upper part of the window is filled with a list box, presenting all LSystem formulas currently known to ChaosPro. You can change the name of each formula simply by selecting it, changing the name in the entry field above the list box and pressing return.
Beneath the list box there are 6 buttons:
-
Load an LSystem formula file: After pressing that button, you are prompted for a formula file containing LSystem formulas to be loaded. ChaosPro is able to read all FractInt LSystem formula files (for example Fractint.l).
-
Save the LSystem formula into a LSystem formula file. This function lets you save the currently selected formula into a formula file. If you specify an existing formula file, then ChaosPro will scan that file, searching for an entry with the same name as the formula to be saved. If an entry is found, ChaosPro asks you, if you want to replace that entry with the currently selected formula, or if you simply want to add your formula to the end of that file.
-
Save All: This function saves all LSystem formulas into a formula file.
-
Delete the currently selected LSystem formula.
-
Add a new LSystem formula.
- Clone the currently selected LSystem formula.
The lower part of the window then allows you to define the formula. The values presented there are those of the formula you selected above in the list.
A formula consists of three parts: The axiom, the angle and a collection of transformation rules.
The axiom is the starting point for the string replacement system. The angle specifies the default angle. Each "+" appearing in any transformation string means rotation by that angle counter clockwise, whereas "-" means rotation by that angle counter clockwise.
Well, if you read and understood the theoretical chapter LSystem Theory, then you know that the whole LSystem scheme simply consists of a string replacement system, appied upto a recursion depth of "maximum number of iterations" (this value you specify in parameter window 1 of a Lindenmayer fractal). And after that number of iterations all you have is a huge string. And this string is interpreted. Following there is the list of commands. If ChaosPro does not know what to do with a character, then it is ignored.
The standard (i.e. most common) drawing commands are:
| F | Draw forward |
| G | Move forward (without drawing) |
| + | Rotate by specified angle counter clockwise |
| - | Rotate by specified angle clockwise |
| | | Turn around 180 degrees |
Normally you should use the commands above. But sometimes you need greater flexibility, and for those cases the following commands exist, which are applied using a totally different angle pointer.
| D | Draw forward |
| M | Move forward (without drawing) |
| \nn | Rotate counter clockwise by nn degrees |
| /nn | Rotate clockwise by nn degrees |
Confusing? Well, in fact, but I had to implement those commands exactly that way in order to be compatible to FractInt. An example:
Angle=4 (i.e. 360/4 degrees=90 degrees)
Axiom: F+FD\45D\90D-F
Rules: No rules
You will see something as follows:
_ \ _/ _|
What happens?
The direction defaults to 0 degree (i.e. points to the right). The current location is at coordinate (0,0), the origin, the line size is 1.
| F | Draw forward by line size using direction 1 | Draw line from (0,0) to (1,0) |
| + | Add 90 degree to direction 1 | Direction 1=90 degree |
| F | Draw forward by line size using direction 1 | Draw line from (1,0) to (1,1) |
| D |
Draw forward by line size using direction 2 Note: The current location is used, but direction 2, i.e. 0 degree, i.e. line to right... |
Draw line from (1,1) to (2,1) |
| \45 | Add 45 degree to direction 2 | |
| D | Draw forward by line size using direction 2 | Draw line from (2,1) to (2.7 , 1.7) |
| \90 | Add 90 degree to direction 2 | |
| D | Draw forward by line size using direction 2 | Draw line from (2.7 , 1.7) to (2, 2.4) |
| - |
Subtract 90 degree from direction 1 è direction 1=0 degree |
|
| F | Draw forward by line size using direction 1 | Draw line from (2, 2.4) to (3, 2.4) |
In order to obtain not only single coloured images, one can change the color. It defaults to index 1 of the current palette and the index into the currently selected palette can be changed by using the following commands.
| Cnn | Select color index nn |
| <nn | Increment color index by nn |
| >nn | Decrement color index by nn |
Some advanced commands, which do not fit into any category above are:
| ! |
Reverse directions, i.e. switch meanings of: + - / \ |
| @nn |
Multiply line size by nn. nn may be preceded by I for inverse or Q for square root, i.e. @Q2 multiplies line size by sqrt(2), and @I3 divides line size by 3. @QI2 divides line size by sqrt(2). |
| [ | Push: Stores current directions (both of them), current position and current color on a stack. |
| ] | Pop: Return to location of last push, i.e. restore that directions, the location and the color. |
Some notes:
The initial line size is not 1, it is 1/(2^maximum iterations). So if you increase the number of iterations, most of the time the LSystem image will be smaller than before, making it necessary to zoom in. FractInt does not know such problems, because FractInt first calculates the LSystem and then adjusts the line size, so the image perfectly fits into the window. But because ChaosPro allows zooming, it must not resize the fractal as FractInt does. And if ChaosPro would leave the line size equal to 1 for each iteration, then the fractal would grow if you increase the number of iterations.