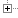Release 4.0

Palette Editor

Adjusting the palette is done in the palette editor. It allows you to adjust the colors, to choose the type of interpolation and to choose the color model. Several preset palettes are provided with ChaosPro, so you should already have some coloring schemes for your fractals. The palette editor looks as follows:

As you can see, there are three display fields, one for each color component (red, green, blue). By looking at a color component you can easily identify the different control points and the interpolation line.

In order to have a common understanding, let's explain and define what a control point actually is:

	Definition: Control Point
	A control point is used as a fulcrum for interpolation. Think of it as follows: Suppose you have a board and a cord. Now you want to place the cord on that board to form some shape. An easy way is to use a hammer and some nails: You drive some nails into the board and then you put the cord alongside the nails. If you then stretch the cord tight, you have a so called "linear interpolation": Line segments ranging from nail to nail, or in technical terms: A linear function between two successing control points. Instead of using a cord you can also use a bendable metal wire: If you conduct the wire alongside the nails you will recognize that it bends around between the nails: Although it touches each nail the whole wire tries to minimize the directional changes: Unlike using linear interpolation by using such a bendable metal wire no sudden directional changes occur. This kind of interpolation is normally called spline interpolation. ChaosPro knows both methods, but both methodsrely on control points.

What can one do with the color components displayed above?

• You can change the colors by dragging control points with the mouse. Your changes are made in realtime, so you will see the effect of dragging a control point to another location even during your drag operation.
• You can add a control point by double clicking into the displayfield onto the position where you would like the control point to be added.
• You can delete a control point by selecting it (clicking onto it using the mouse) and then pressing the DEL key or the BACKSPACE key on your keyboard.
• You can perform drag or delete operations on multiple control points at the same time by using "multiselect": Simply click into the displayfield, hold down the mouse key and move the mouse around: A selection rectangle will appear. Drag it, so it covers the control points you'd like to be selected. While holding down the SHIFT key on your keyboard you then can preserve the selection and drag all selected control points around.
  
  Holding down the SHIFT key on the keyboard will generally preserve the selection state of the control points. So you can multiselect control points by holding down the SHIFT key and selecting each control point separately: It will then be added to the current selection list.

To the left and right side of each displayfield there is a so called "color simulator": It shows you what would happen if you would move the current control point up or down.

Below the displayfields there is the offset slider: This slider allows you to displace the palette.

And below the offset slider at the left edge of the palette editor there is the color selector: It displays the current color. By clicking onto the filled circle another window will open which allows you to choose a color using the HSL color wheel.

The items beneath the color selector let you view or manually adjust the color values.

And the last item in the palette editor is the Smooth checkbox. If it is not checked, then the control points are interpolated using linear interpolation. Otherwise the control points are interpolated using a limited cubic spline (i.e. a smooth curve).